cumulativehypotheses

Suppose we were to take methods one by one, at random and without replacement, from the source code of Hudson 2.1.0 How would we expect the Cyclomatic Complexity of those methods to be distributed?

Here you will find some automation to discover the raw numbers, and here is a Mathematica Computable Document (get the free reader here) showing the analysis. If you have been playing along so far you might expect the distribution of complexity to follow a power law.

Result:

This evidence suggests that the Cyclomatic Complexity per method in this version of Hudson is not distributed according to a discrete power–law distribution (the hypothesis that it is, is rejected at the 5% level).

Probability of Complexity of Methods in Hudson

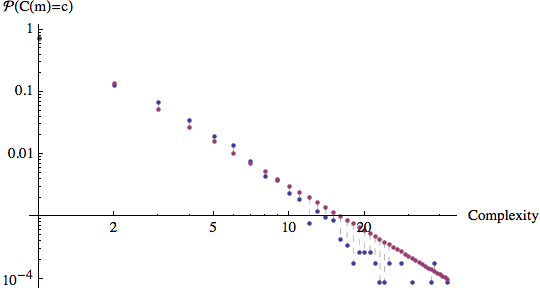
This chart shows the empirical probability of a given complexity in blue and that from the maximum–likelihood fitted power–law distribution in red. Solid lines show where the fitted distribution underestimates the probability of methods with a certain complexity occurring, dashed lines where it overestimates. As you can see, the fit is not great, especially in the tail.

Note that both scales are logarithmic.

Other long-tailed distributions (e.g. log-normal) can be fitted onto this data, but the hypothesis that they represent data is rejected at the 5% level.